| Page 1 of 1 |
|
|
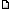 Posted: Wed, 4th Nov 2015 13:37 Post subject: Linear Algebra Posted: Wed, 4th Nov 2015 13:37 Post subject: Linear Algebra |
|
 |
Hi guys...
I don't know if we have any math experts at our hands but I have some "homework" in linear algebra and it's been too long since I had that shit at university so any help would be appreciated: (beware, shitty translation in ms paint  ) )

Thanks 
|
|
| Back to top |
|
 |
|
|
 Posted: Wed, 4th Nov 2015 13:41 Post subject: Posted: Wed, 4th Nov 2015 13:41 Post subject: |
|
 |
|
|
|
| Back to top |
|
 |
|
|
|
| Back to top |
|
 |
|
|
|
| Back to top |
|
 |
|
|
 Posted: Wed, 4th Nov 2015 16:39 Post subject: Posted: Wed, 4th Nov 2015 16:39 Post subject: |
|
 |
Please obi wan barnsen, tell me how2usewolframalpha for any of those questions
|
|
| Back to top |
|
 |
|
|
|
| Back to top |
|
 |
TSR69
Banned
Posts: 14962
Location: Republic of the Seven United Provinces
|
|
| Back to top |
|
 |
|
|
 Posted: Wed, 4th Nov 2015 20:29 Post subject: Posted: Wed, 4th Nov 2015 20:29 Post subject: |
|
 |
Me yes but not my wife 
|
|
| Back to top |
|
 |
|
|
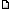 Posted: Wed, 4th Nov 2015 20:58 Post subject: Posted: Wed, 4th Nov 2015 20:58 Post subject: |
|
 |
Does \lambda_1 v_1 mean some inner product? I am not used to the notation.
|
|
| Back to top |
|
 |
Nui
VIP Member
Posts: 5720
Location: in a place with fluffy towels
|
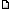 Posted: Wed, 4th Nov 2015 21:55 Post subject: Posted: Wed, 4th Nov 2015 21:55 Post subject: |
|
 |
For (2) one needs to show these two things right? Let the defined space be X.
1. a,b \in X \Rightarrow a+b \in X
addition of two elements is another element
2. a \in X, s \in K, s*a \in X
a scaled element is another element
latex for the solution?
 Spoiler: Spoiler: |
copy it here if you want: http://www.artofproblemsolving.com/texer
| Code: | Let $X$ be the defined space; $a,b \in X$; $s \in K$. Requirement one, $a + b \in X$:
\begin{align}
a + b
&= \left( a_1 + b_1, \ldots, a_n + b_n \right) \\
&\rightarrow \left( (a_1 + b_1) v_1 + \cdots + (a_n + b_n) v_n \right) \\
&= \underbrace{\left( a_1 v_1 + \cdots + a_n v_n \right)}_{0, a \in X}
+ \underbrace{\left( b_1 v_1 + \cdots + b_n v_n \right)}_{0, b \in X} \\
&= 0 \\
&\Rightarrow a + b \in X
\end{align}
Requirement two, $s \cdot a \in X$:
\begin{align}
s \cdot a
&= \left( s a_1, \ldots, s a_n \right) \\
&= \left( s a_1 v_1 + \cdots + s a_n v_n \right) \\
&= s \cdot \underbrace{\left( a_1 v_1 + \cdots + a_n v_n \right)}_{0, a \in X} \\
&= 0 \\
&\Rightarrow s \cdot a \in X
\end{align} |
|
|
|
| Back to top |
|
 |
|
|
 Posted: Thu, 5th Nov 2015 00:26 Post subject: Posted: Thu, 5th Nov 2015 00:26 Post subject: |
|
 |
uh
i can do linear algebra but proofs? fuck that
i want to do code, not prove shit i already know
so i never learnt any proofs and somehow managed to pass my cs math
|
|
| Back to top |
|
 |
|
|
 Posted: Thu, 5th Nov 2015 00:59 Post subject: Posted: Thu, 5th Nov 2015 00:59 Post subject: |
|
 |
| Nui wrote: | For (2) one needs to show these two things right? Let the defined space be X.
1. a,b \in X \Rightarrow a+b \in X
addition of two elements is another element
2. a \in X, s \in K, s*a \in X
a scaled element is another element
latex for the solution?
 Spoiler: Spoiler: |
copy it here if you want: http://www.artofproblemsolving.com/texer
| Code: | Let $X$ be the defined space; $a,b \in X$; $s \in K$. Requirement one, $a + b \in X$:
\begin{align}
a + b
&= \left( a_1 + b_1, \ldots, a_n + b_n \right) \\
&\rightarrow \left( (a_1 + b_1) v_1 + \cdots + (a_n + b_n) v_n \right) \\
&= \underbrace{\left( a_1 v_1 + \cdots + a_n v_n \right)}_{0, a \in X}
+ \underbrace{\left( b_1 v_1 + \cdots + b_n v_n \right)}_{0, b \in X} \\
&= 0 \\
&\Rightarrow a + b \in X
\end{align}
Requirement two, $s \cdot a \in X$:
\begin{align}
s \cdot a
&= \left( s a_1, \ldots, s a_n \right) \\
&= \left( s a_1 v_1 + \cdots + s a_n v_n \right) \\
&= s \cdot \underbrace{\left( a_1 v_1 + \cdots + a_n v_n \right)}_{0, a \in X} \\
&= 0 \\
&\Rightarrow s \cdot a \in X
\end{align} |
|
|
Oh thanks, I'll try and see how this turns out  |
|
| Back to top |
|
 |
Nui
VIP Member
Posts: 5720
Location: in a place with fluffy towels
|
|
| Back to top |
|
 |
|
|
 Posted: Thu, 5th Nov 2015 08:59 Post subject: Posted: Thu, 5th Nov 2015 08:59 Post subject: |
|
 |
Since I only know R I have just set K = R throughout :/ and I am not really good at the abstract stuff. Here is my try on the first 2 anyway.
(2) Everything follows using the properties of the inner produkt. ( basically what nui did). We have a set of vectors given by \lambda \cdot \mathbf{v} = 0, så (\lambda_1 + \lambda_2) \cdot \mathbf{v} = yada yada due to inner product.
(3) Linear independence means that the matrix of vectors on an arbitrary vector given by (v1,v2,...,vn)\mathbf(K) = 0
leads to K_i = 0. So diagonalize the matrix and the multiplication of \mu will only be in the diagonal so the set is still independent.
|
|
| Back to top |
|
 |
| Page 1 of 1 |
All times are GMT + 1 Hour |